2.1 算法的时间复杂性分析
算法的时间复杂性分析是一种事前分析估算的方法,他是对算法消耗的资源的一种渐进性分析方法。
渐进性分析:只关注输入规模增大时算法运行时间的增长趋势。
2.2 输入规模与基本语句
输入规模:指输入量的多少。
基本语句:执行次数与整个算法执行次数成正比的语句,基本语句对算法运行时间的贡献最大,是算法中最重要的操作。例如下行代码:
int SeqSearch(int A[],int n,int k)
{
for(int i=0;i<n;i++)
if(A[i] == k) break; //基本语句是这个比较操作A[i] == k
if(i == n) return 0;
else return (i+1);
}
//输入规模是带炸找的记录个数n
//更多例子,查找课本P18页内容2.3算法的渐进分析
定义:若存在两个正的常熟c和n。对于任意的n >= N,都有T(n) <= c*f(n);则称T(n) = O(f(n)) <或者称算法在 O(f(n))中> 。
渐进分析要分析最坏,最好,平均情况。
★非递归算法的时间复杂性分析:确定问题的输入规模,找出算法的基本语句,检查基本语句的执行次数是否只依赖输入规模,建立基本语句执行次数的求和表达式,用渐进符号表示这个求和表达式(用大O表示)。
★递归算法的时间复杂性分析:递归就是将地推关系中等式的右边的项根据递推式进行替换。举例:
{ 7 n = 1
T(n) = {
{ 2T(n/2) + 5n^2 n > 1解:T(n) = 2T(n/2) + 5n^2 = 2(2T((n/2)/2 + 5(n/2)^2 +5n^2 = 2(2(2T(n/8) + 5(n/4)^2) + 5(n/2)^2) + 5n^2 .... = 2^k*T(1) + 2^(k-1)*5(n/(2^(k-1)) + ... + 2*5(n/2)^2 + 5n^2
最终表达为:T(n) = 7n + 5n^2(2-1/2^(k-1)) = 10n^2-3n <= 10n^2 = O(n^2)
2.4 算法的空间分析
指的是算法在执行过程中需要的的辅助空间的数量,算法临时开辟的存储空间。例如起泡算法初始序列与排序结果都在r[n]中,在排序算法运行过程中设置了三个简单的变量,因此算法的空间复杂度为O(1),但是对于P19 例2.3来说空间复杂度就是N+M。
2.5 最优化算法
问题的计算复杂性下界:指计算这个问题所需的最小工作量,任何求解该问题的算法的时间复杂度都不会低于这个下界。
判定树模型:满足两个条件的二叉树,一是每一个内部结点对应一个形如x<=y的比较,如果关系成立,则控制转移到该结点的左子树,否则,控制转移到该结点的右子树;二是每一个叶子结点表示问题的一个结果,在用判定书模型建立问题的时间下界时,通常忽略求解问题的所有算数运算,只考虑执行分支的转移次数。
例题
下列算法的基本语句,执行了多少次,算法的时间复杂性?
int Stery(int n)
{
int S = 0;
for (int i = 1; i <= n; i++)
S = S + i * i;
return S;
}基本语句: s=s+i*i; 执行了n次; 算法的时间复杂性O(n)。
int Q(int n)
{
if (n == 1)
return 1;
else
return Q(n-1) + 2 * n - 1;
}基本语句: Q(n-1)+2*n-1; 执行了n次; 算法的时间复杂性O(n)。
for (i = 1; i <= n; i++)
if (2*i <= n)
for (j = 2*i; j <= n; j++)
y = y + i * j;基本语句: 2*i <=n和y=y+i*i; 都执行了n/2次; 算法的时间复杂性O(n)。
基本语句找执行次数与整个算法执行次数成正比的,算法复杂度:带N就是O(n),N^2就是O(n^2).找N的最高次。
使用扩展递归技术求解下列递推公式
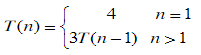
int T(int n){
if(n==1)
return 4;
else if(n>1)
return 3*T(n-1);
}简单来说就是两个if区分开n的定义域,然后分别返回对应的计算式。



Comments NOTHING